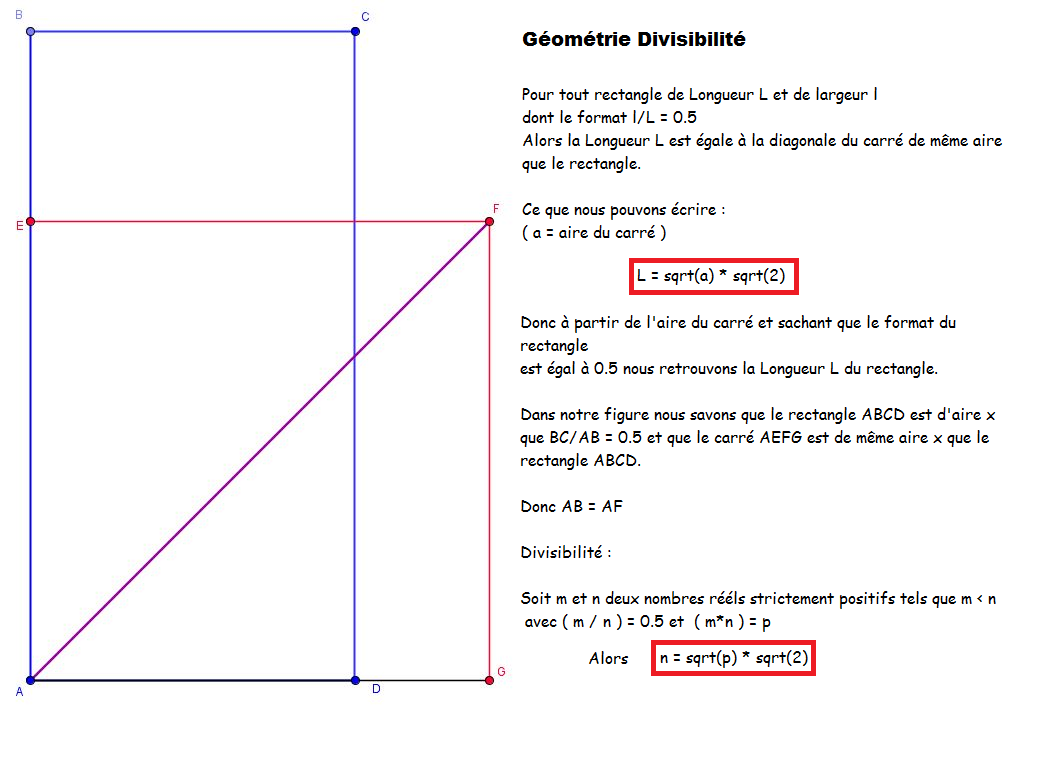
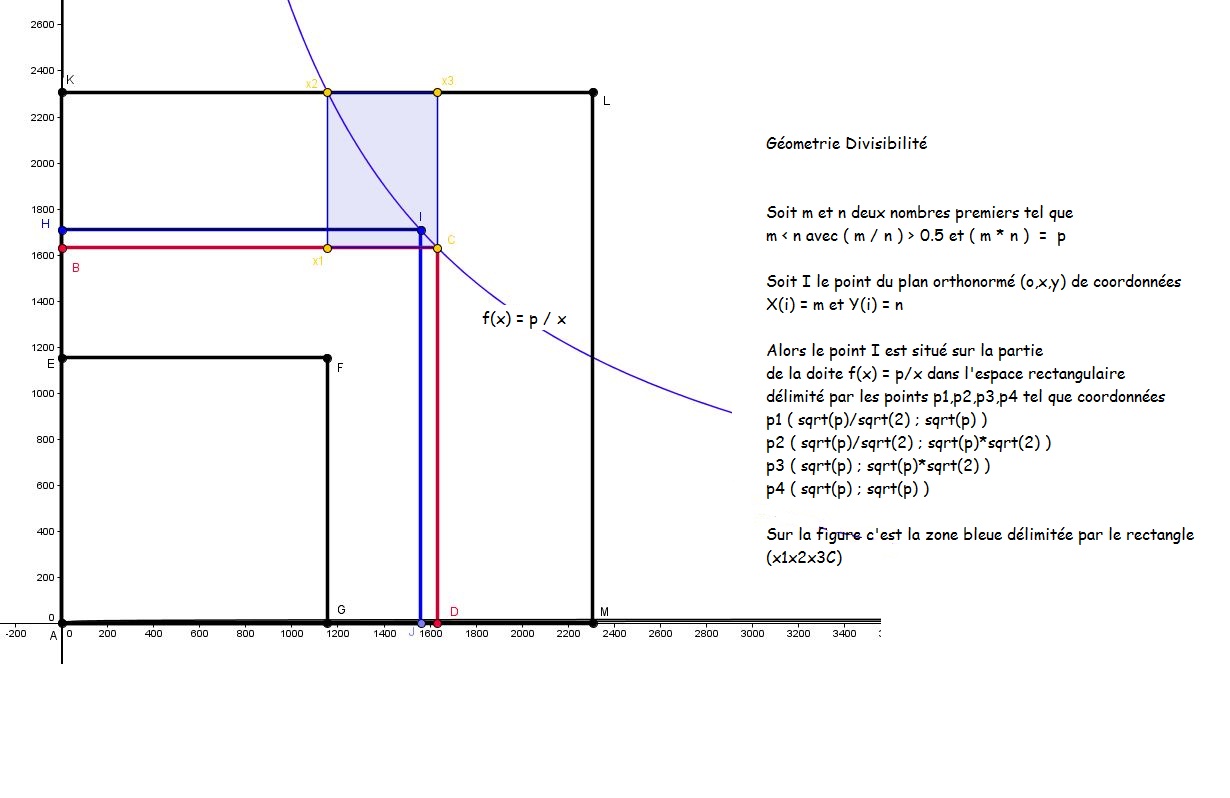
Pour tout nombre réel p différent de 0 tel que p = | m * n | avec |m| < |n|
Alors :
soit |m| / |n| = 0.5
soit |m| / |n| < 0.5
soit |m| / |n| > 0.5
Si |m| / |n| = 0.5 alors |m| = √p * √2
Si |m| / |n| > 0.5 alors il existe au moins un couple de nombres réels m et n facteurs de p
tel que
√p / √2 < |m| < √p < |n| < √p * √2
Si |m| / |n| < 0.5 alors il existe au moins un couple de nombres réels m et n facteurs de p
tel que
|m| < √p / √2 et |n| > √p * √2
Pour tout nombre semi-premier p tel que p = m * n avec 2 < m < n alors l’intervalle de définition du rapport m/n est ]0 ; 0.5[ U ]0.5 ; 1[
Si m/n > 0.5
Alors √p / √2 < m < √p < n < √p * √2
Et
Si m/n < 0.5
Alors m < √p / √2 et n > √p * √2
Réciproquement pour un nombre semi-premier p tel que p = m * n avec 2 < m < n
Si √p / √2 < m < √p ou √p < n < √p * √2
Alors m/n > 0.5
Et si m < √p / √2 ou n > √p * √2
Alors m/n < 0.5