Un algorithme basé sur la multiplication scolaire

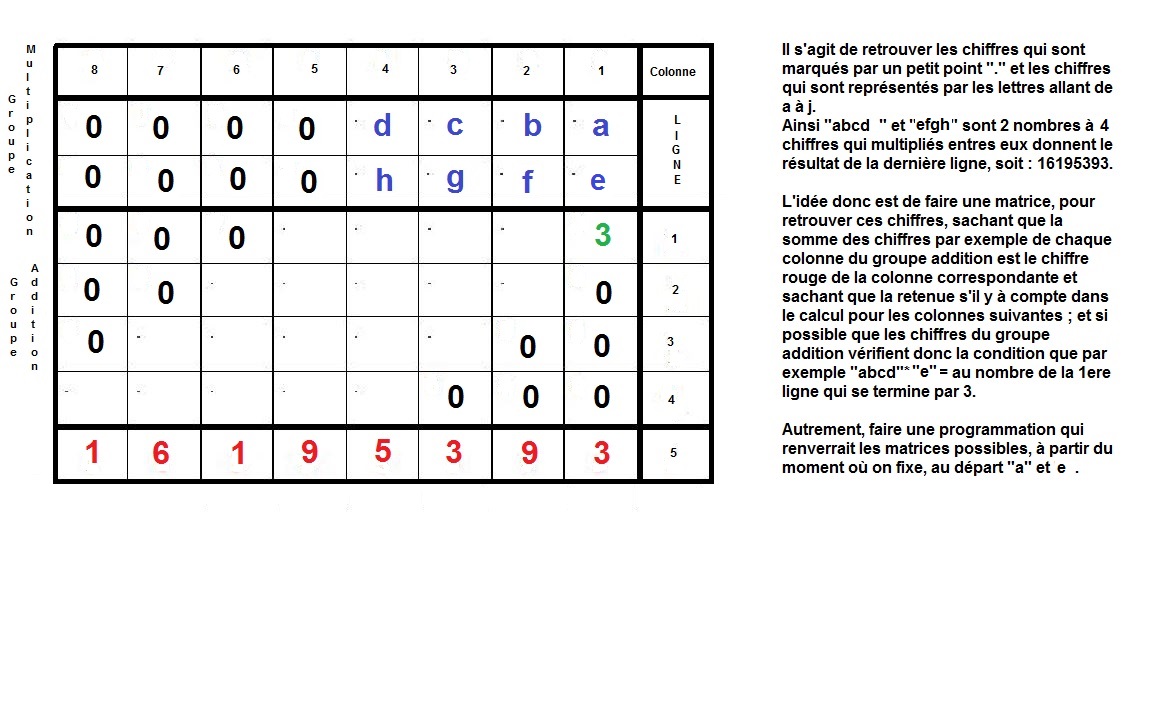
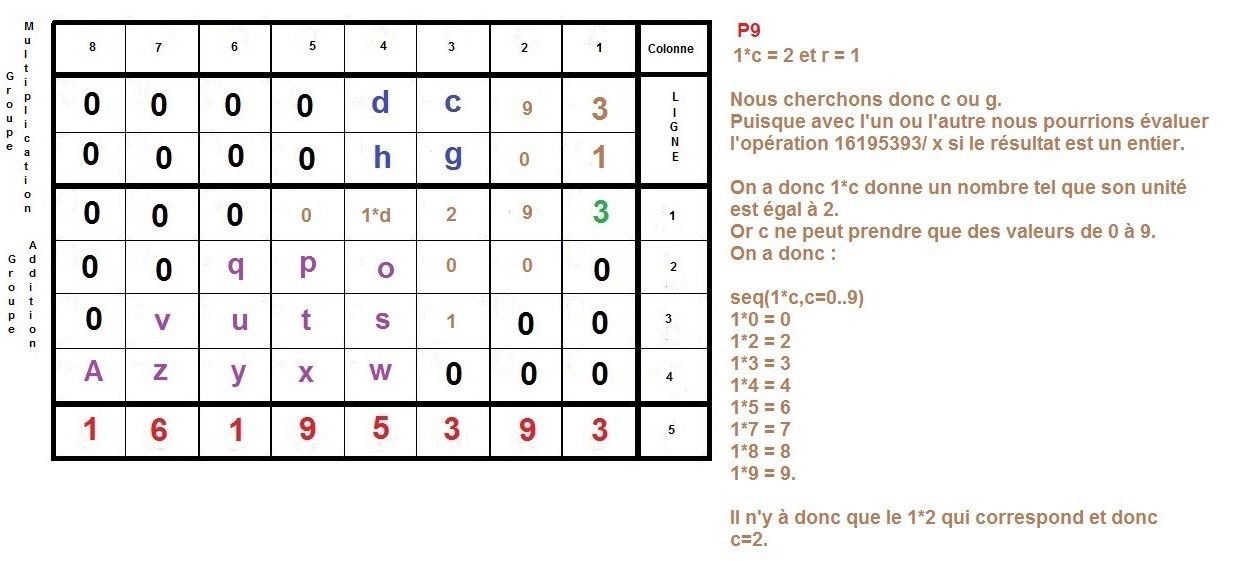
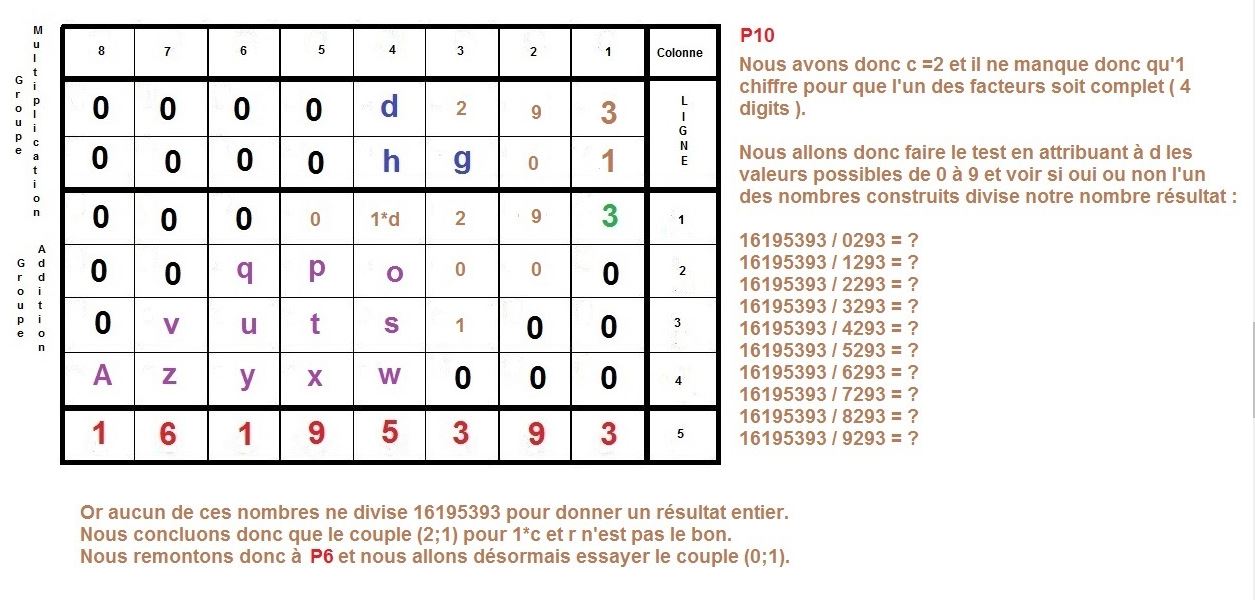
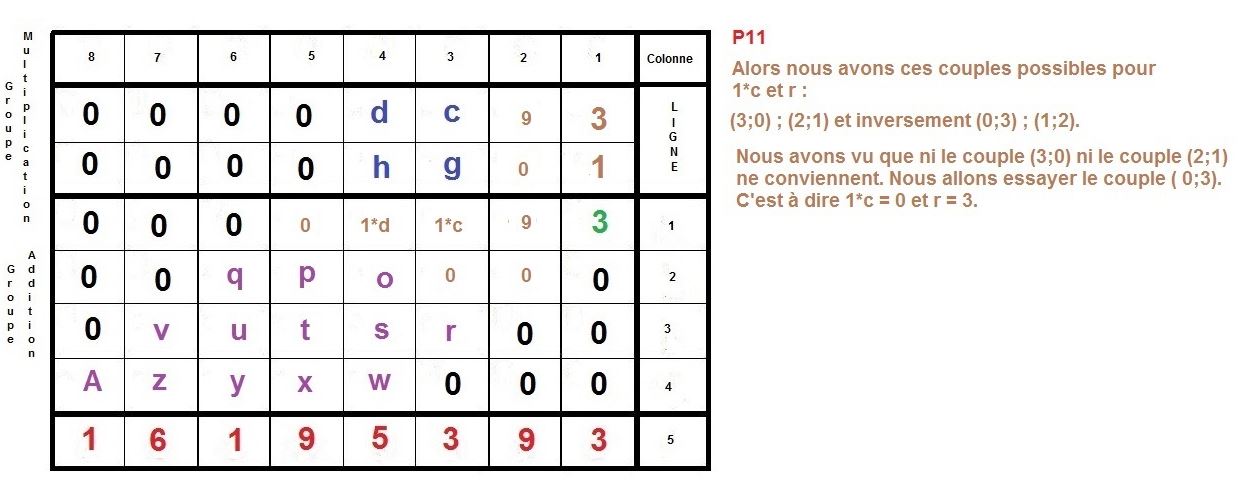
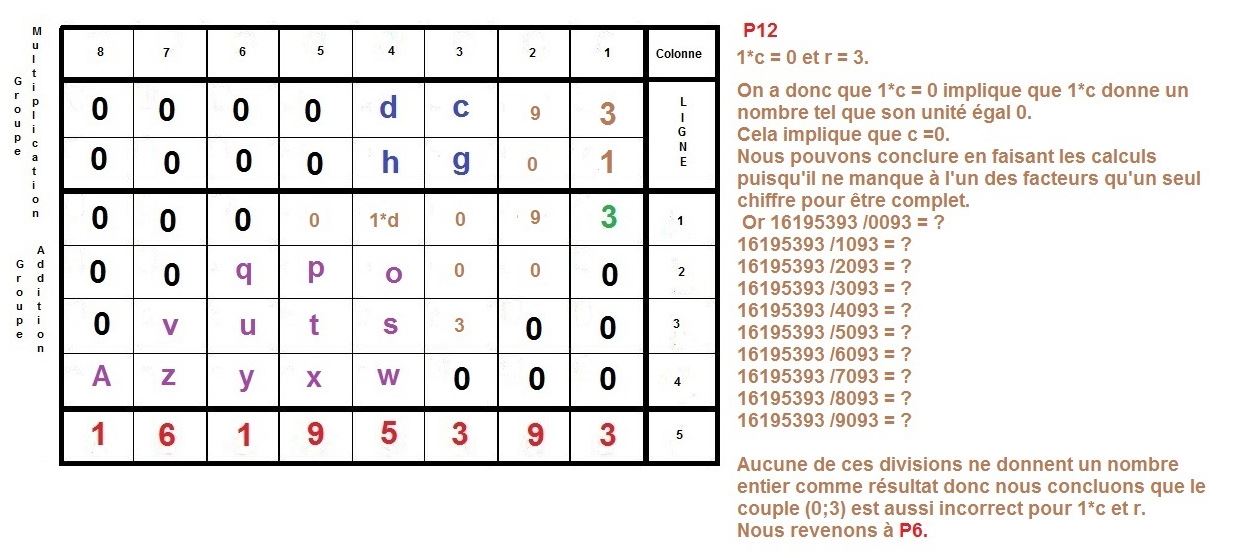
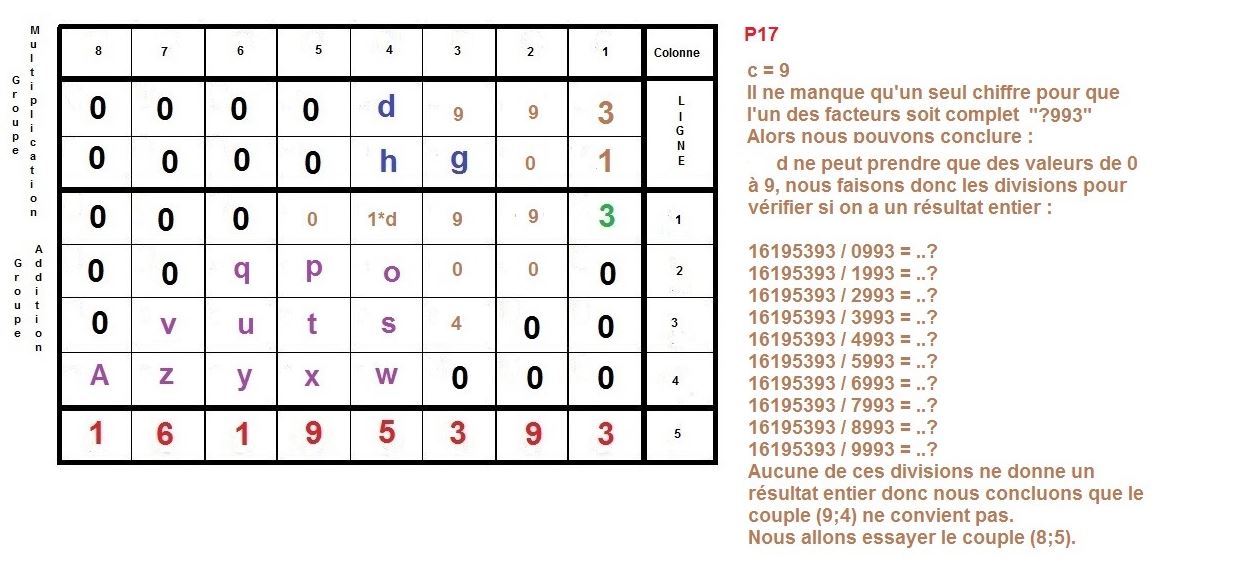
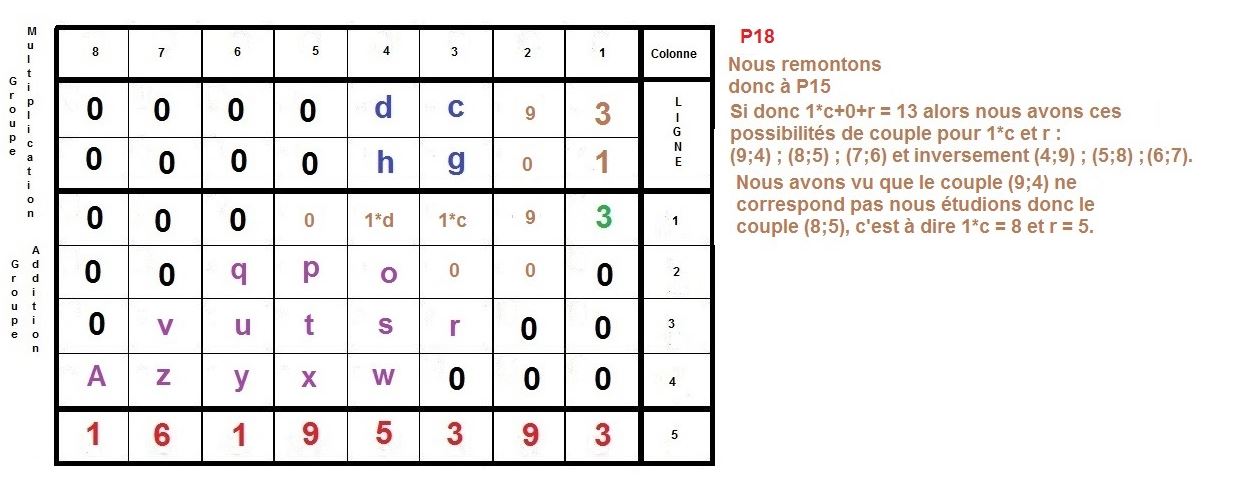
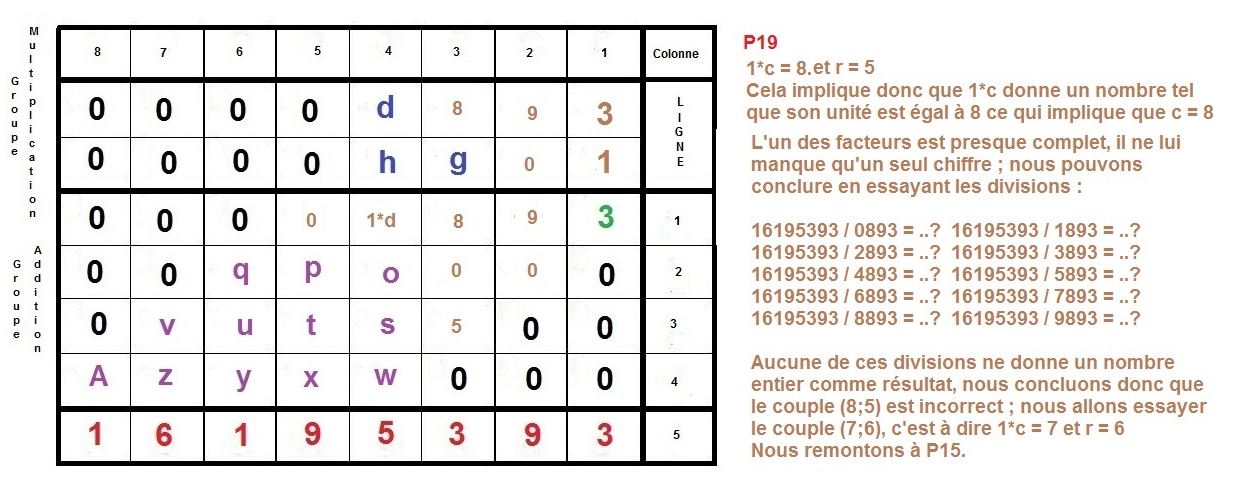
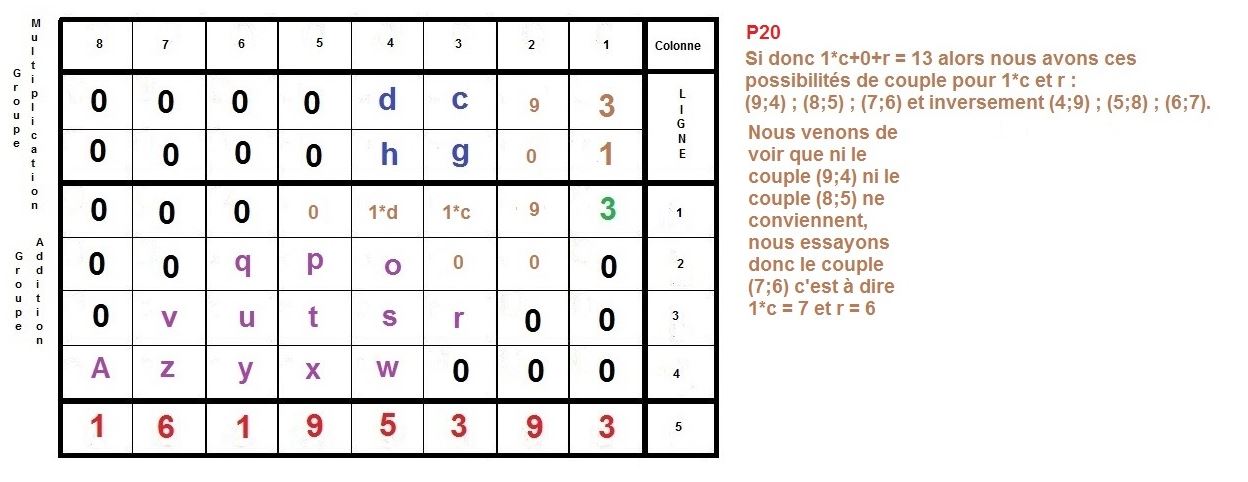
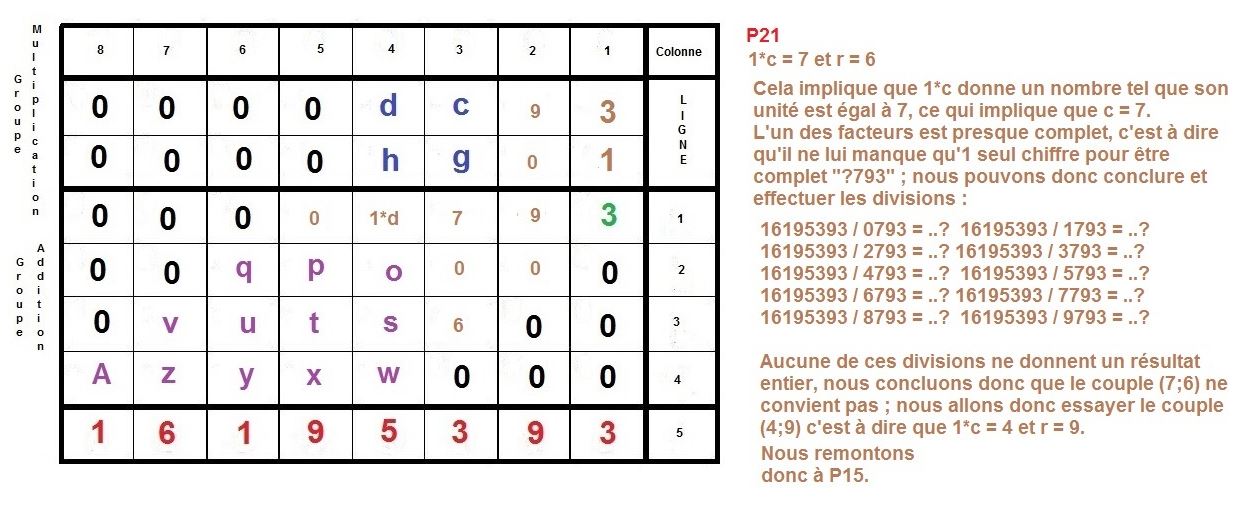
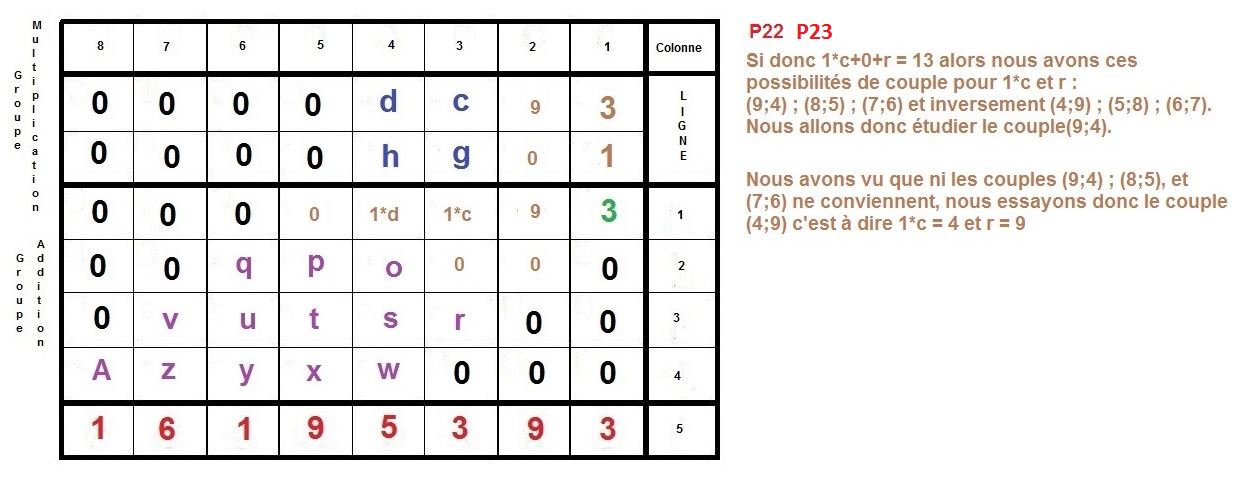
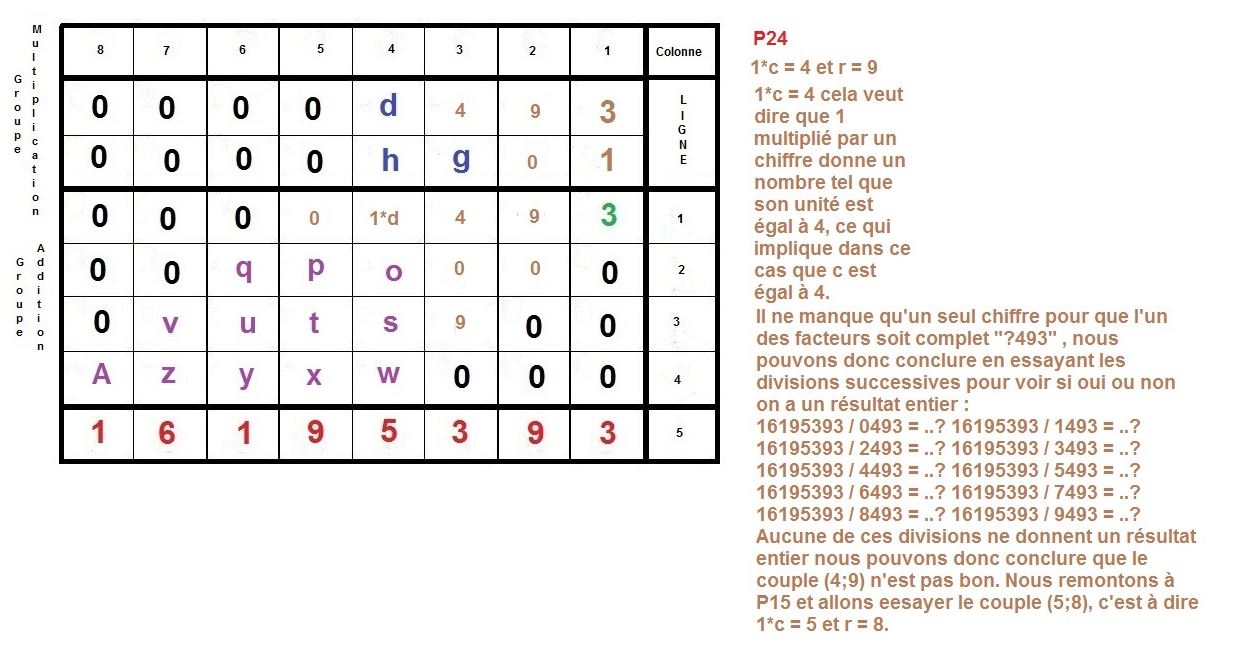
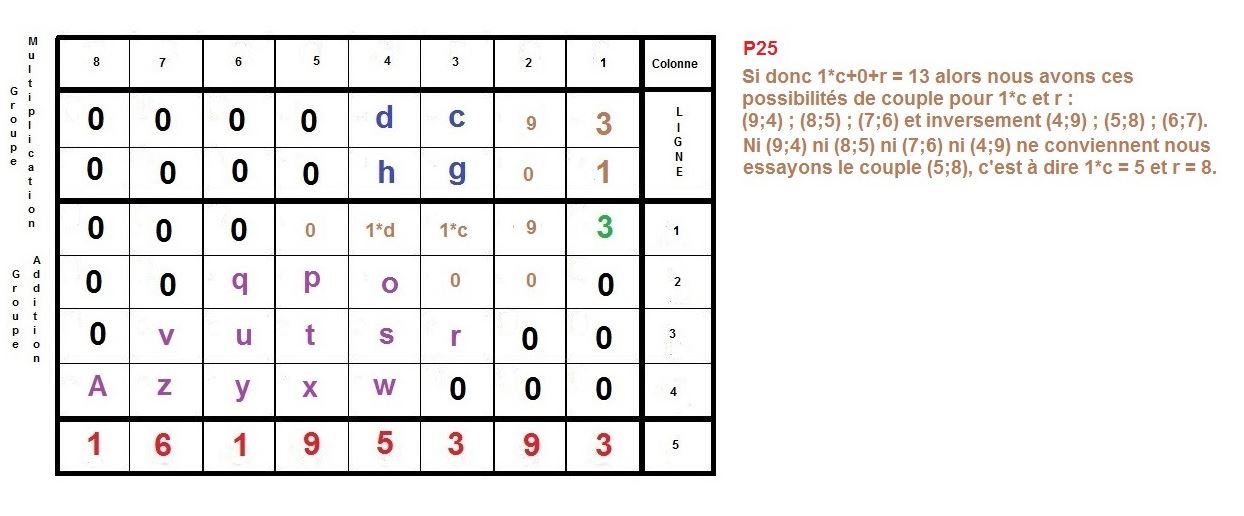
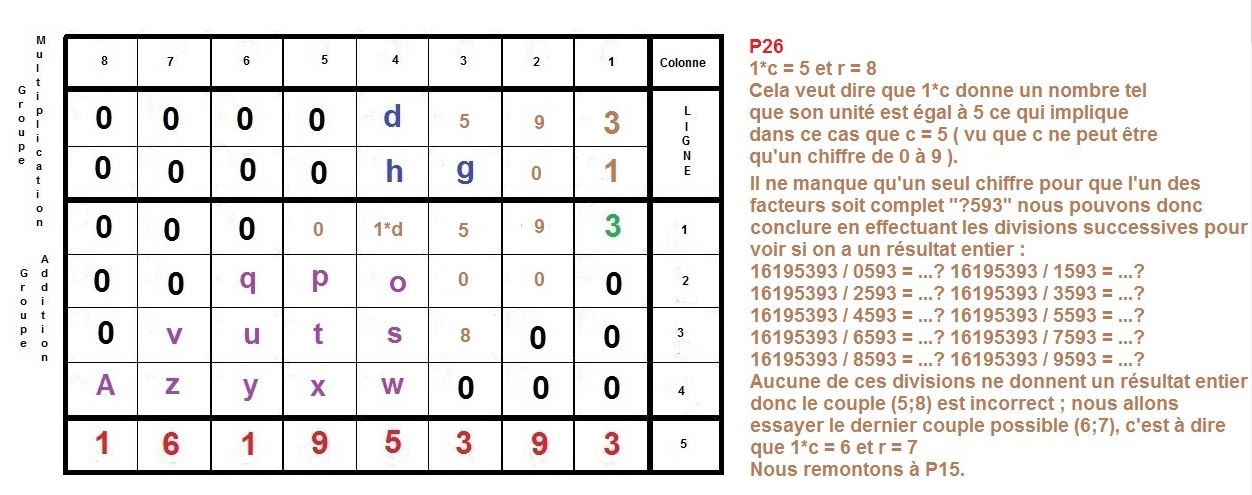
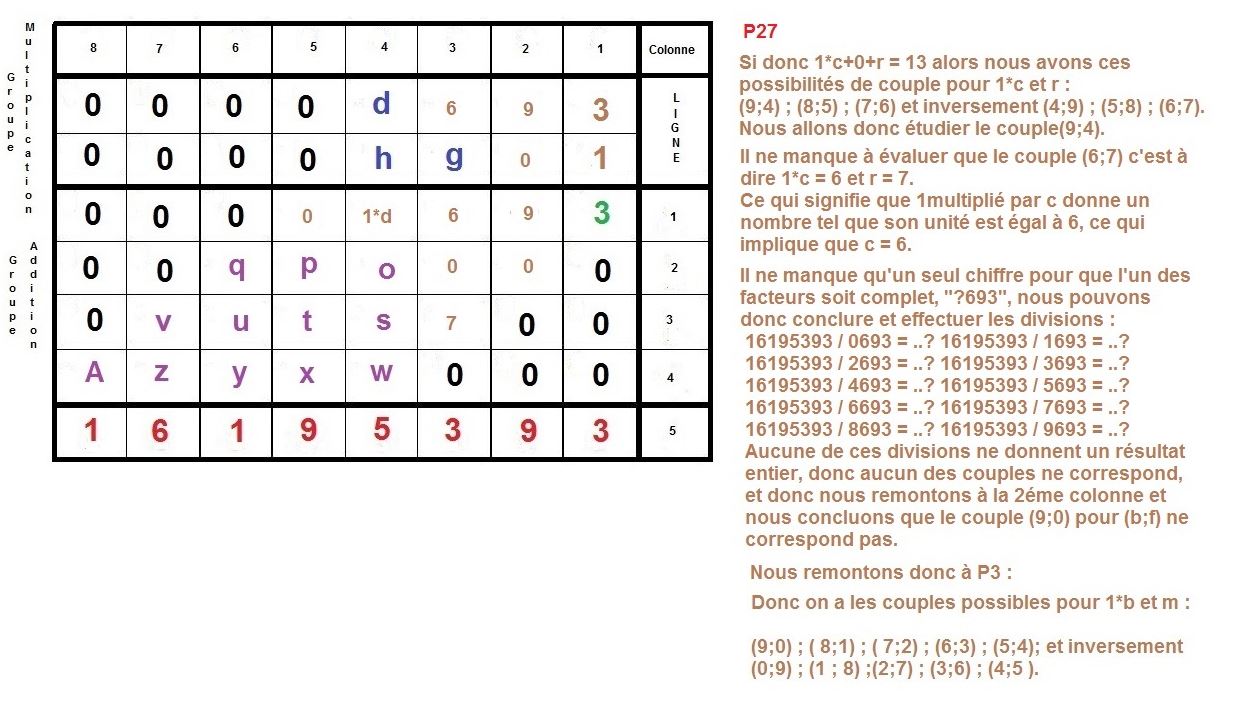
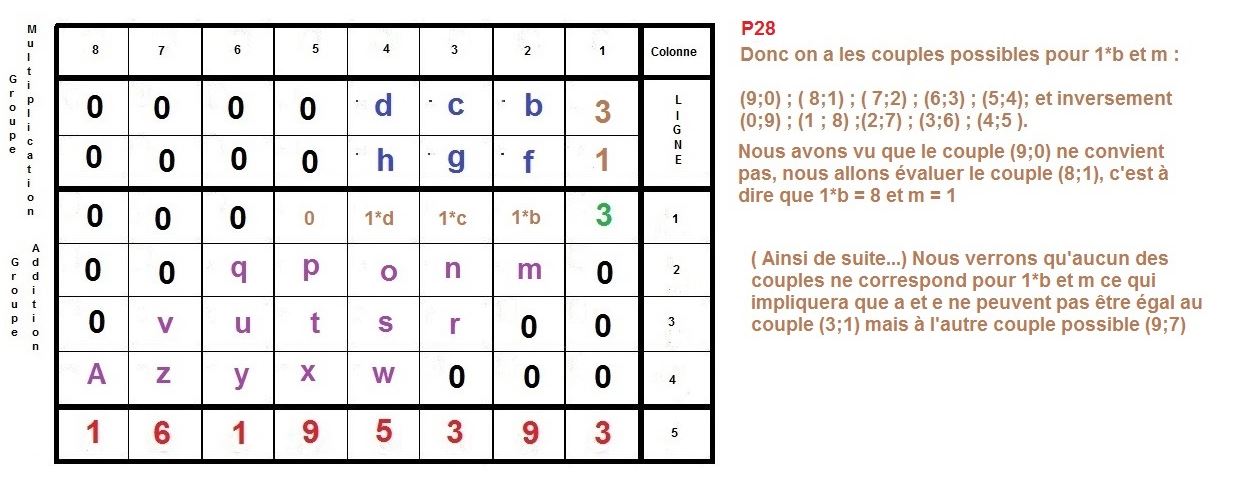
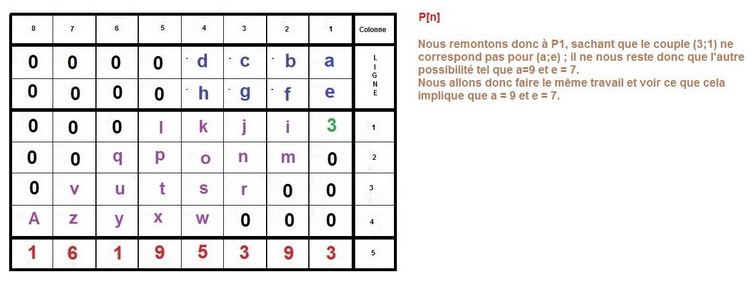
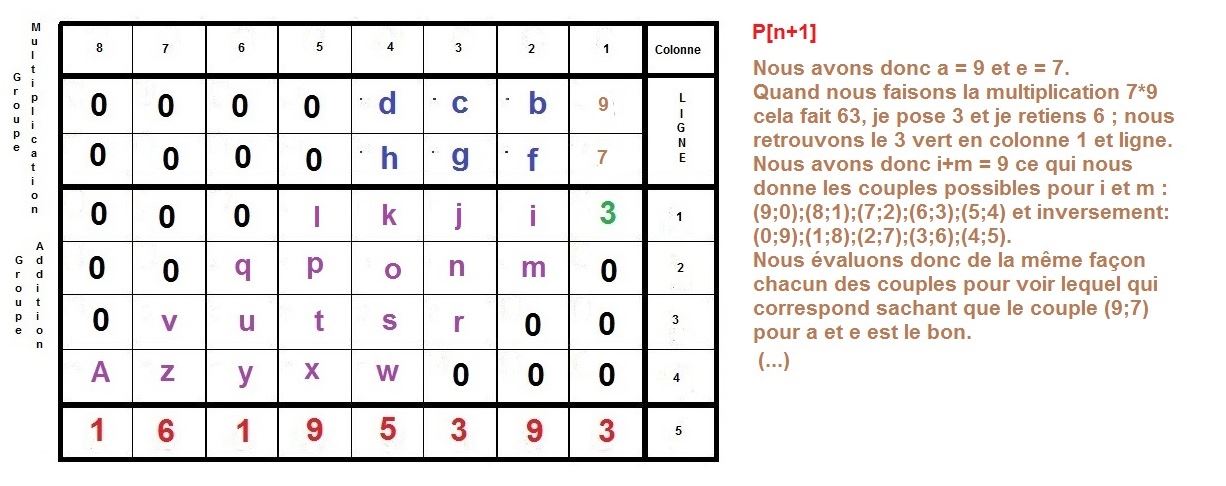
L’idée est de faire la construction inverse d’une multiplication à la main, qu’on apprend en classe élémentaire.
Il s’agit de partir du résultat de la multiplication, et de retrouver donc, les deux facteurs premiers, d’un nombre semi-premier.
Ici, nous nous intéressons à des cas où ces deux facteurs sont égaux en terme de longueur décimale, c’est à dire qu’ils sont composés du même nombre de chiffres.

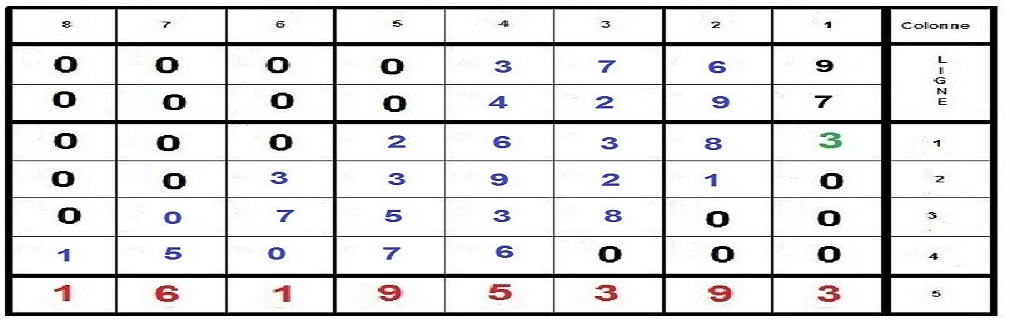
Nous allons prendre l’exemple des nombres 3769 et 4297 qui sont composés du même nombre de décimales, c’est à dire de 4 chiffres.
Faisons la multiplication classique de ces 2 nombres :

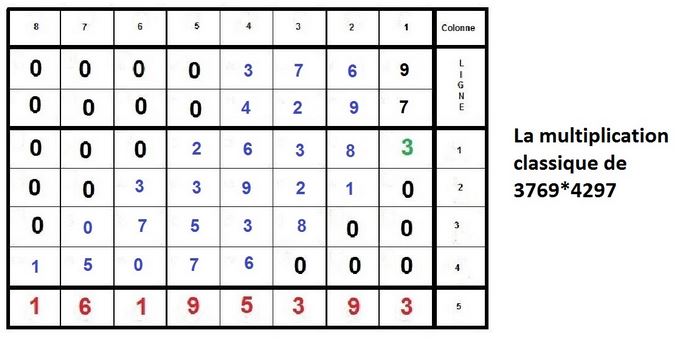
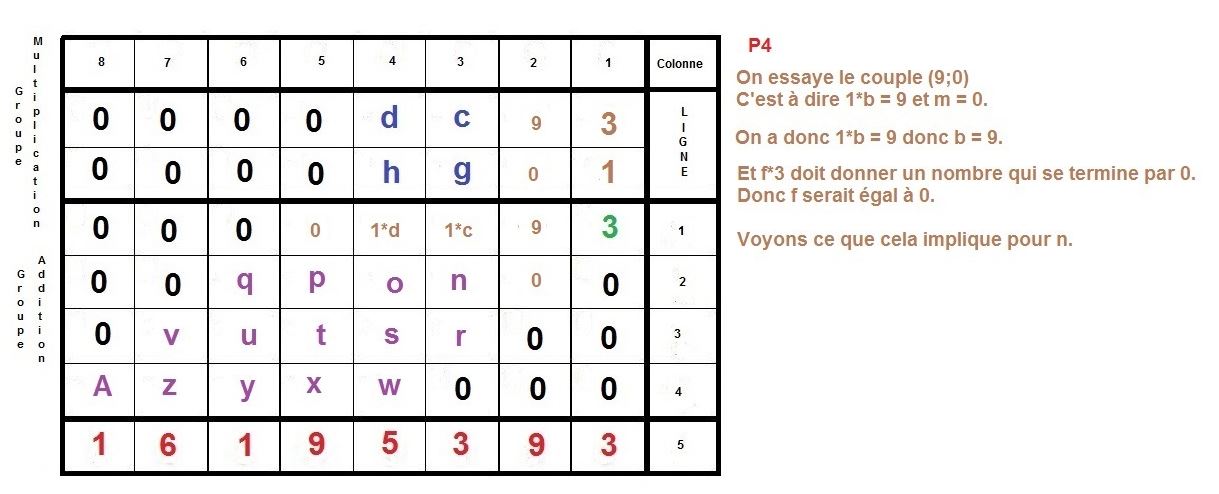
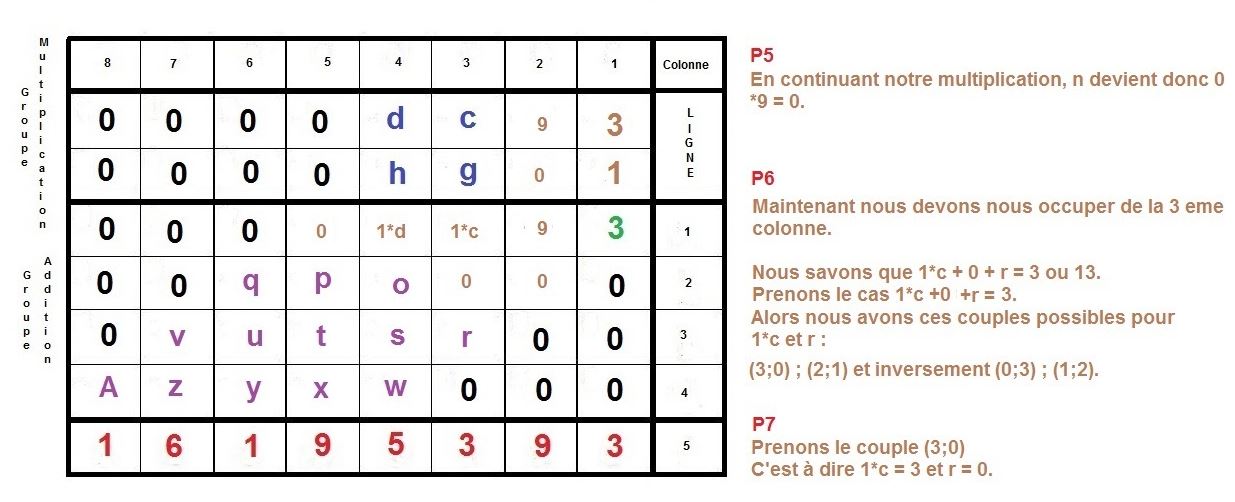
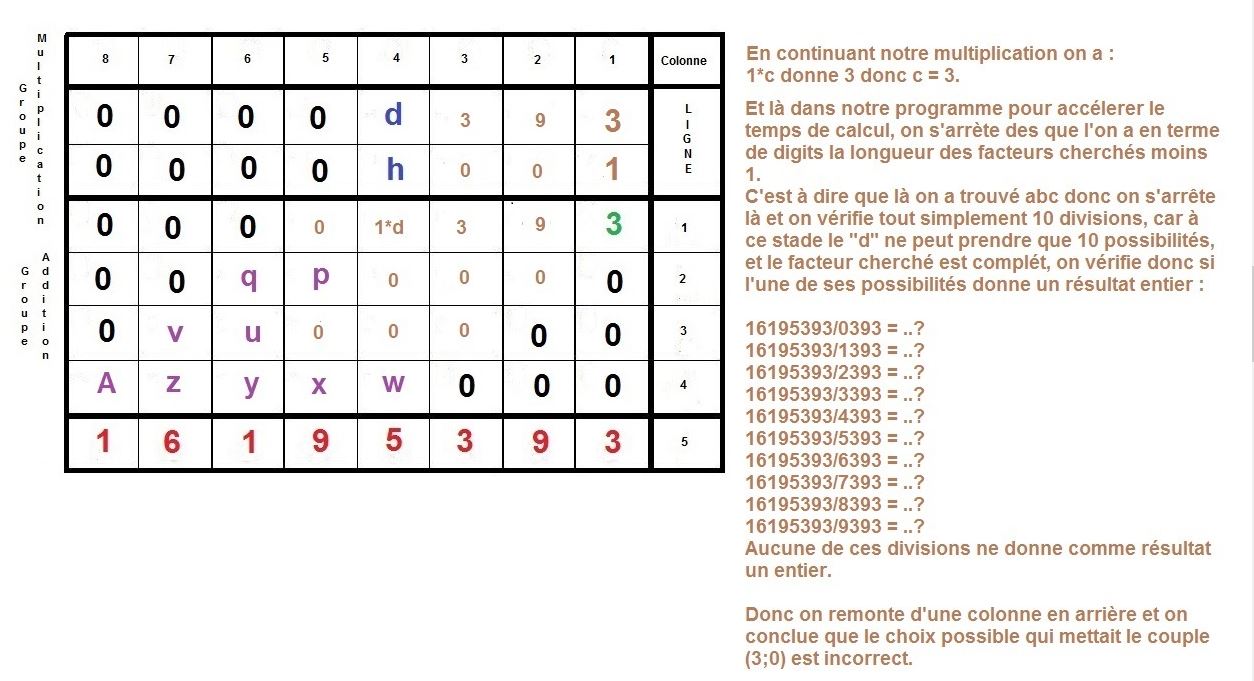
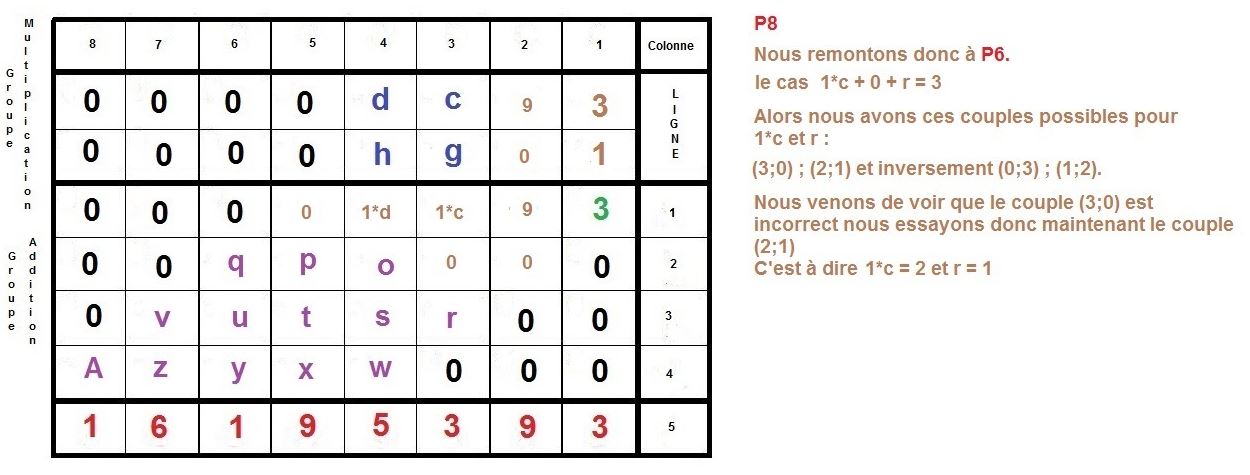
Maintenant, nous allons procéder à l’inverse, nous partirons du résultat 16195393 pour remonter aux 2 facteurs :

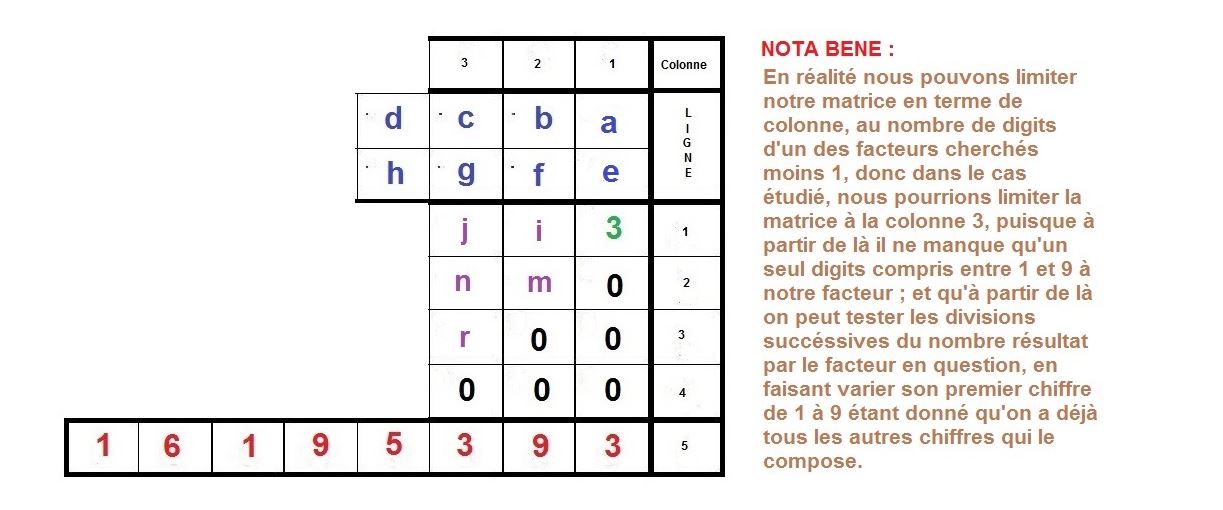
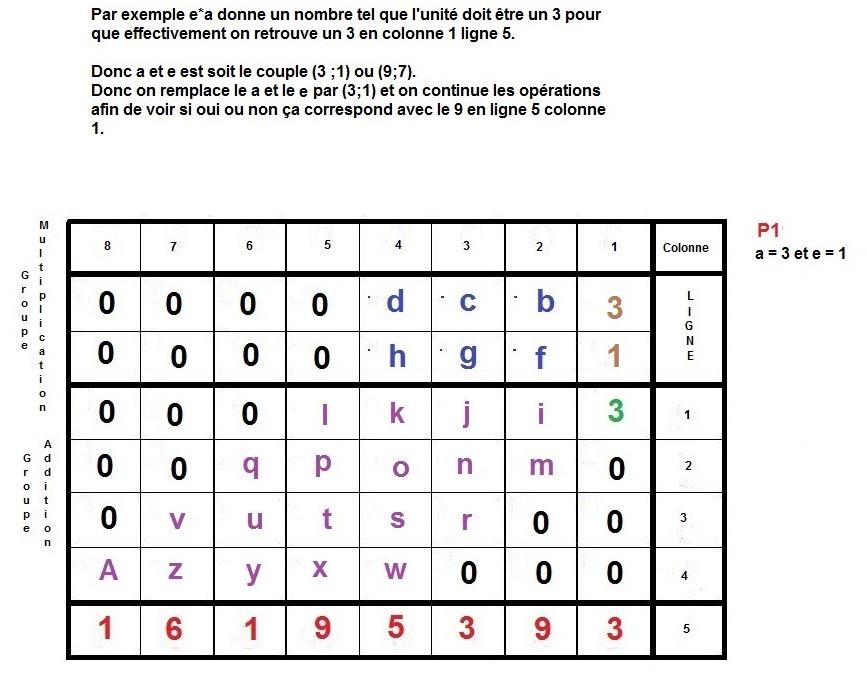
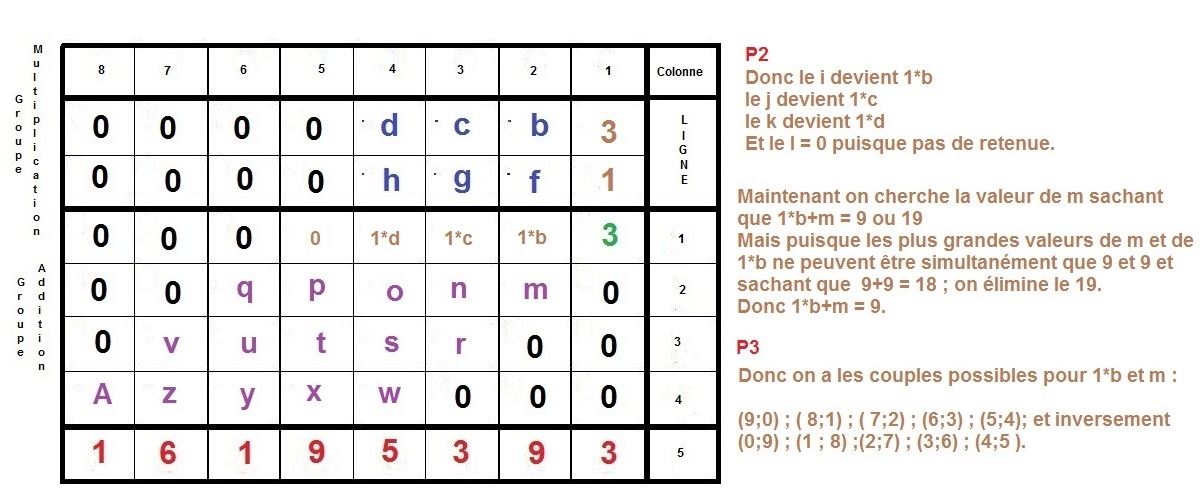
Voilà donc une possibilité, afin d’élaborer un algorithme se basant sur la technique de multiplication qu’on apprend à l’école élémentaire.

restart;
Digits:=1000;
“©Algorithme Guimzo-ALS Tous droits réservés “;
construit_matrice := proc (N::posint, M::posint, O::posint) local mat, nb, i, j, reste, div, ligne;
mat := matrix(N+3, 2*N);
nb := M;
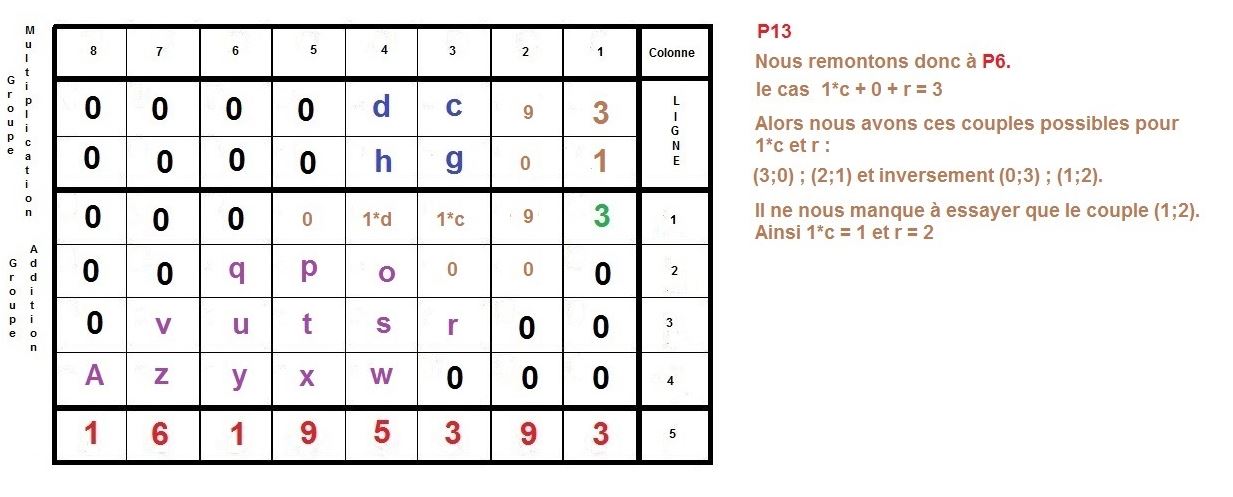
for i to length(nb) do reste := `mod`(nb, 10);
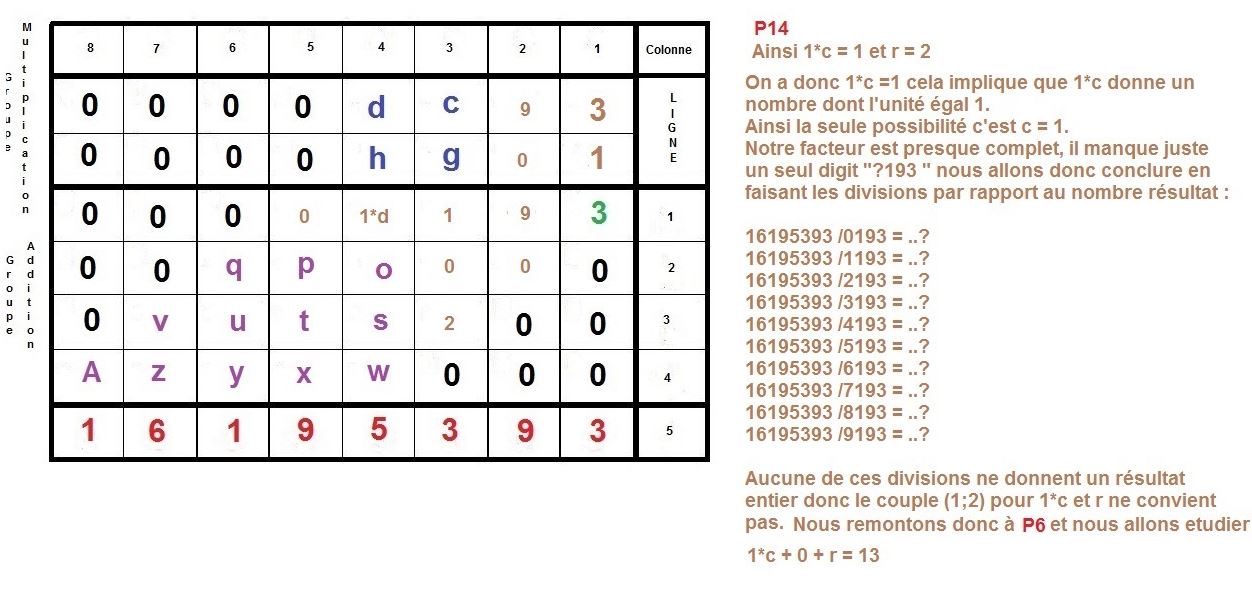
mat[N+3, 2*N+1-i] := reste;
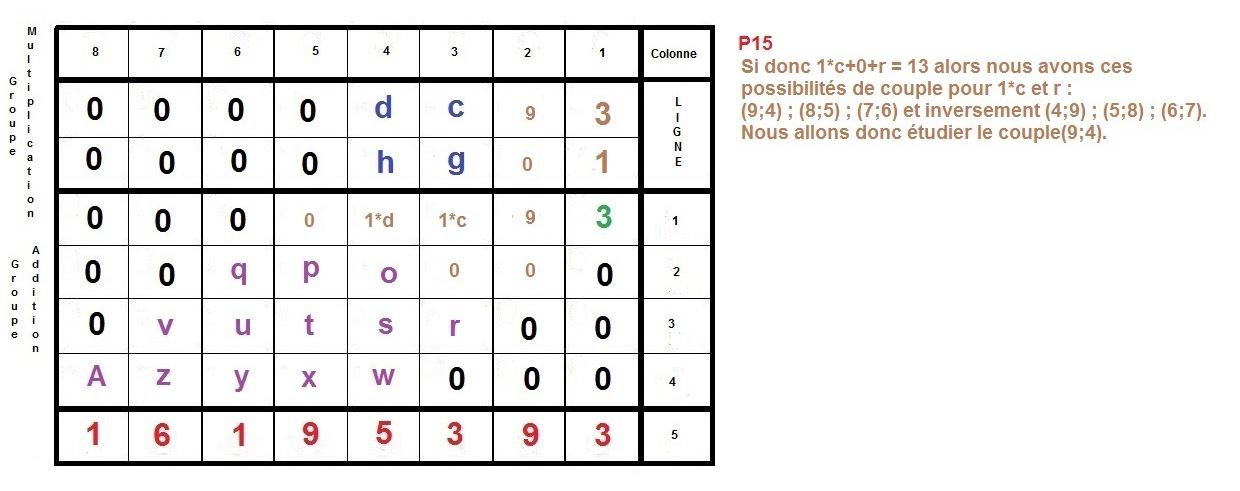
nb := (1/10)*nb-(1/10)*reste end do;
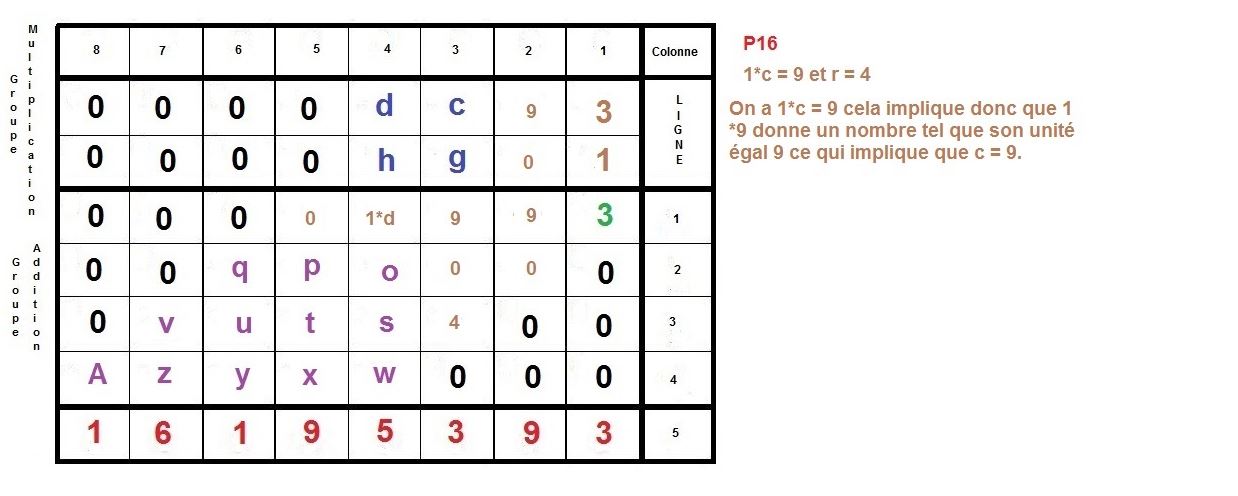
div := NULL;
for i in numtheory[divisors](M) do if length(i) = N then div := div, i end if end do;
div := [div];
for ligne to 2 do for i to N do mat[ligne, i] := 0 end do;
for i to N do reste := `mod`(div[ligne], 10);
mat[ligne, N+i] := reste;
div[ligne] := (1/10)*div[ligne]-(1/10)*reste end do end do;
mat[3, 2*N] := O;
j := 0;
for ligne from 3 to 2+N do j := j+1;
for i to N-j do mat[ligne, i] := 0 end do end do;
j := 0;
for ligne from 4 to 2+N do j := j+1;
for i to j do mat[ligne, 2*N+1-i] := 0 end do end do;
evalm(mat) end proc;
construit_matrice(4, 16195393, 9)